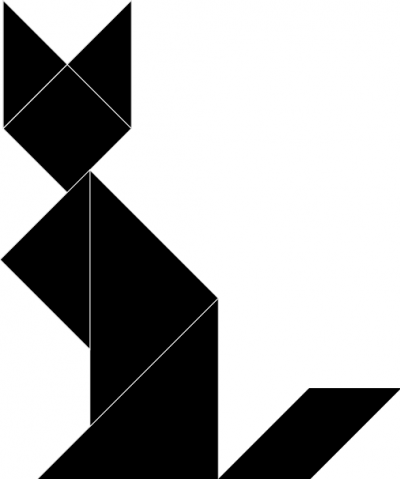Il tangram è un antico gioco di origine cinese, ottenuto scomponendo un quadrato in sette parti dette tan: un quadrato, un romboide, e cinque triangoli rettangoli isosceli, di cui due grandi, uno medio e due piccoli.
Combinando opportunamente i pezzi del Tangram, è possibile ottenere un numero pressoché infinito di figure, alcune geometriche, altre che ricordano oggetti d’uso comune, ecc. Qualsiasi figura realizzata con il Tangram deve essere costituita impiegando tutti i sette pezzi.
Tangram is an ancient game of Chinese origin, obtained by breaking down a square into seven parts called tan: a square, a rhomboid, and five isosceles right-angled triangles, two of which are large, one medium and two small.
By appropriately combining the pieces of the Tangram, it is possible to obtain an almost infinite number of figures, some geometric, others reminiscent of everyday objects, etc. Any figure made with Tangram must be made up using all seven pieces.
Ecco un esempio risolto di Tangram. Questo è un gatto realizzato con tutti i sette pezzi. Tramite le linee bianche vedrete facilmente la posizione dei pezzi.
This is a solved Tangram example. This is a cat figure made from all seven pieces. Through the white lines you will easily find the pieces’s positions.
Ora tocca a te! Prova a ricreare queste figure componendole con tutti i sette pezzi del TANGRAM.
Now it’s your turn! Try to recreate these figures by composing them with all seven pieces of the TANGRAM.
Alcune considerazioni e osservazioni matematiche:
Quali altre riesci a vedere?
Some mathematical considerations and observations:
What others observations can you see?